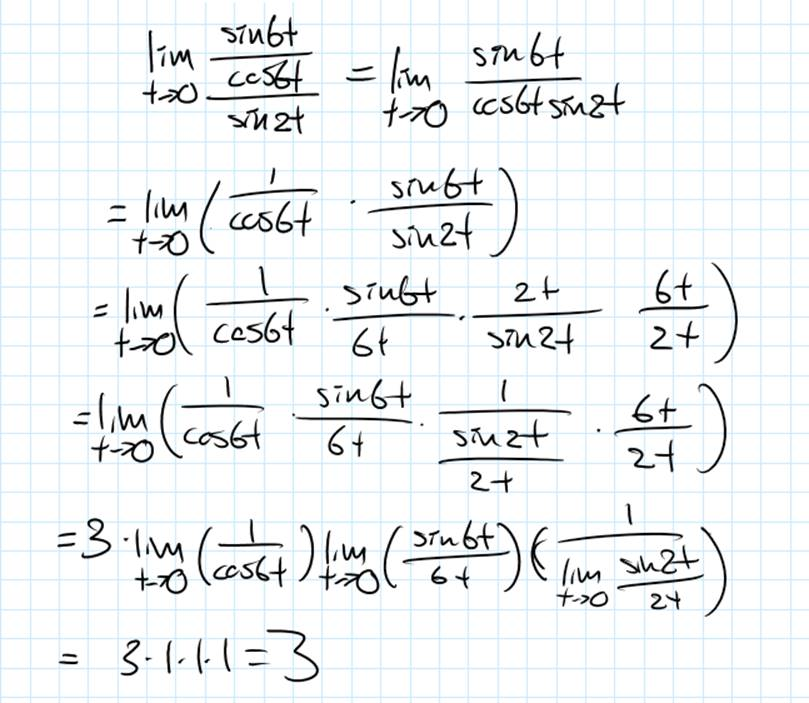Borbin the 🐱

My cat asked me for a staircase. After a long design discussion he finally said: "meow"! Project is on!

All parts except the round material were cut from those boards.

The boards were cut in length.

And to thinner size.

The staircase has an angle of 30°

With a fixed vise all the holes in the treads were drilled.

One of the wooden rounds broke and I had to cut one manually. Took longer than expected.

The railing holes are cut with a 30° alignment using one of the cut offs as a guide.

Two parts assembly.

Construction finished. Painting!

Customer is happy!

It is his staircase.

It was in one of the first physics courses when the Prof used 22/7 in an equation as an approximation. Within a few steps, he calculated the result on the board, leaving us students astounding about this.

So simple, and yet so close:

22 / 7 = 3,1̅4̅2̅8̅5̅7

𝜋 = 3,14159265358

22 / 7 - 𝜋 ≈ 0,00126

The math department would not had approved this, but not us engineers!

For Math126 we were talking about the Taylor series for

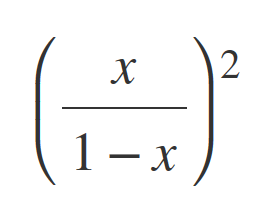
It looks difficult at first glance, but it is actually quite simple. Let me explain:

Using this as a base:

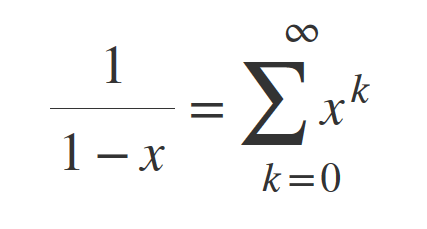
The derivative of this term is:

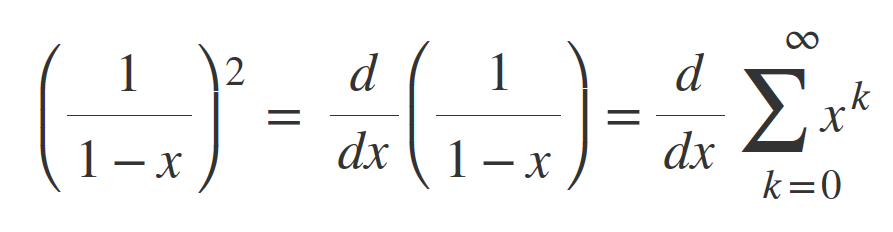
Which gets to:

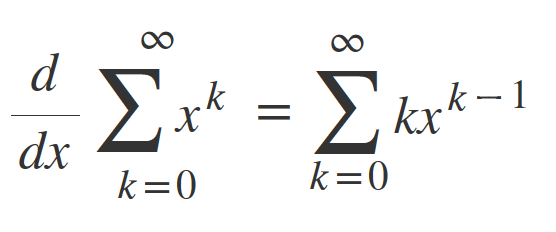
Now move the nominator in the sum to get the solution:

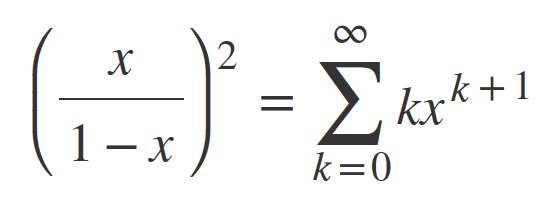
Time for a small PowerShell script for the Taylor series:

function f([double]$x)
{
    [Math]::Pow($x/(1-$x), 2)
}

function T([double]$x, [int]$k)
{
    0..$k | % { $sum = 0 } { $sum += $_ * [Math]::Pow($x, $_ + 1) } { $sum }
}


[int]$K = 16

for([int]$xi = -5; $xi -le 5; $xi += 1)
{
    [double]$x = $xi / 10

    [PSCustomObject]@{
        'x' = $x
        'f(x)' = f $x
        'T(x)' = T $x $K
    }
}

   x                f(x)                T(x)
   -                ----                ----
-0,5   0,111111111111111   0,111068725585938
-0,4  0,0816326530612245  0,0816318326348185
-0,3  0,0532544378698225  0,0532544328723274
-0,2  0,0277777777777778  0,0277777777741005
-0,1 0,00826446280991736 0,00826446280991734
   0                   0                   0
 0,1  0,0123456790123457  0,0123456790123457
 0,2              0,0625  0,0624999999943475
 0,3   0,183673469387755   0,183673459741776
 0,4   0,444444444444445   0,444442421037629
 0,5                   1   0,999862670898438

The convergence is | x | < 1
T₁₅ is used for this test.

 k             Tk(x)
 -             -----
 0                 0
 1              0,25
 2               0,5
 3            0,6875
 4            0,8125
 5          0,890625
 6            0,9375
 7        0,96484375
 8        0,98046875
 9      0,9892578125
10       0,994140625
11    0,996826171875
12    0,998291015625
13  0,99908447265625
14     0,99951171875
15 0,999740600585938

The Altas 7B shaper is a rare metal shaper dating back 70+ years. Even more rare is the optional indexer.
And a perfect new project to replicate this rotary indexer for my Atlas shaper!

While browsing eBay for some suitable round table with t-nuts I could use to get started for the project, I found this:

An original S7-425 rotary indexer table! Arrived a few days later:

With the top of the indexer covered, I needed material for the base. Lots of 3/4" thick 8" round plate available at eBay:

But a few mm to large for the lathe. To get the jaws a good grip and to pass the bed of the lathe, I had to cut out the four sides to make it fit.

Cutting out the hole for the plate:

This setup is for the engraving. With a insert for cutting threads, the degree ticks were done. A simple wood block ensured a constant length of the tick marks. Once done, the 5 and 10 degree marks were done with a slightly larger depth.

First part of the base is finished.

The final one:

To evaluate the limit, we apply standard trigonometric identities to decompose the expression into terms involving sin⁡(x)/x​ for which a limit for x→0 exists.
While algebraic manipulation to eliminate the denominator is sometimes effective, it is not applicable in this case.
Instead, recognizing and leveraging this fundamental limit allows for a straightforward and elegant solution.